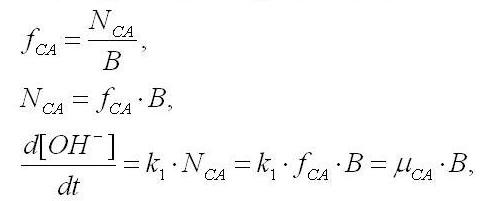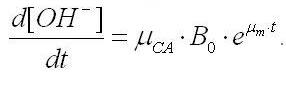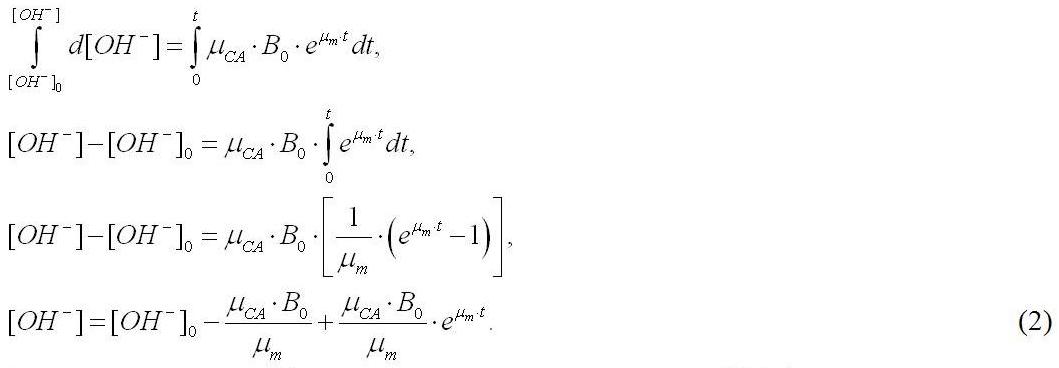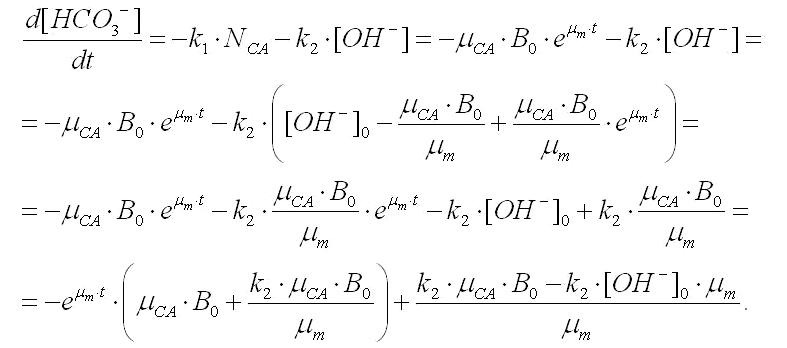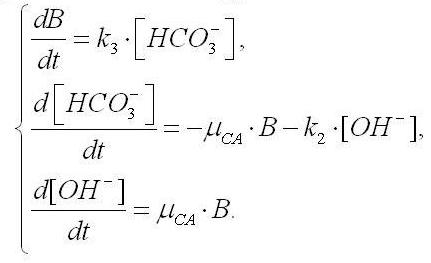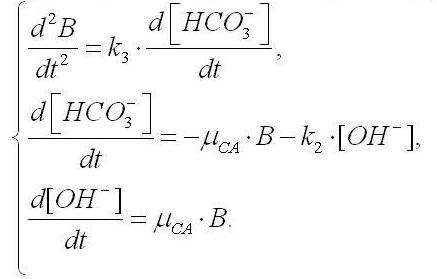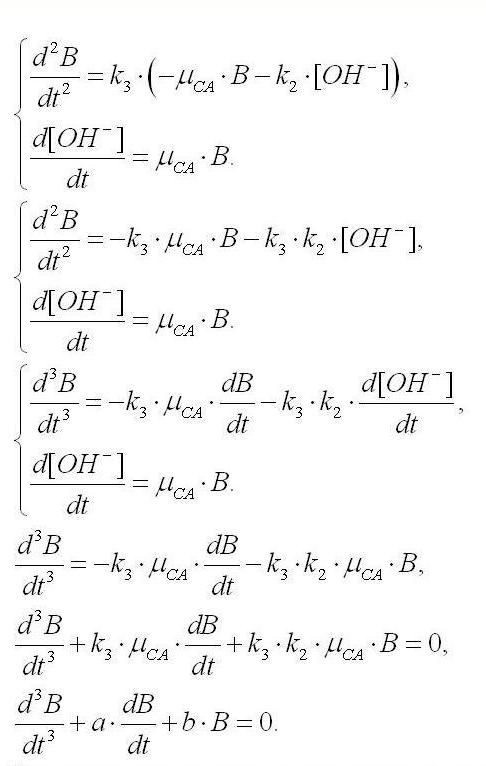по Материалам Международной конференции «Экологическая физиология водных фототрофов: распространение, запасы, химический состав и использование»
V Сабининские чтения 29 ноября 2016 - 29 января 2017
Моделирование динамики роста Arthrospira (Spirulina) platensis и рН среды
в закрытой по углероду системе
Modeling the dynamics of growth of Arthrospira (Spirulina) platensis and pH
in a carbon closed system
Лелеков А.С., Геворгиз Р.Г.
Alexander S. Lelekov, Ruslan G. Gevorgiz
Институт морских биологических исследований им. А.О. Ковалевского (г. Севастополь)
УДК 579.017.8:57.036
Предложена математическая модель роста накопительной культуры A. platensis в условиях закрытой по углероду системы. Модель позволяет объяснить остановку роста плотности культуры при наличии в среде около половины внесенного углерода и других биогенных элементов. Показано, что при экспоненциальном росте культуры молярная концентрация гидроксил-ионов в среде увеличивается экспоненциально, при этом концентрация гидрокарбонат ионов снижается не только экспоненциально, но и линейно. Модель основана на известных представлениях о метаболизме углерода в клетке и его ассимиляции из культуральной среды.
Ключевые слова: микроводоросли; математическая модель; рН культуральной среды; лимитирование углеродом
Введение
Культуры низших фотоавтотрофов часто используются в качестве модельного объекта при исследовании вопросов влияния различных факторов среды на скорость роста популяции. Одним из модельных объектов при изучении процессов фотобиосинтеза является цианобактерия Arthrospira platensis (синоним – Spirulina platensis), которая широко известна под названием спирулина. Благодаря простоте технической реализации большинство экспериментальных работ со спирулиной осуществляется в накопительном режиме культивирования. По форме накопительной кривой можно судить о лимитирующих рост факторах внешней среды, а также о последовательности их действия (Лелеков, Тренкеншу, 2007). Рост накопительной культуры есть сложный динамический процесс, в ходе которого происходят постоянные изменения как биохимического состава клеток, так и состава среды. Следовательно, необходимо принимать во внимание влияние совокупности нескольких факторов на скорость роста культуры. При культивировании спирулины в условиях накопительной культуры одним из ключевых факторов, определяющих форму кривой роста, является углеродное обеспечение. При условии оптимальных световых условий и температуры скорость роста будет определяться концентрацией основных биогенных элементов в питательной среде. Обычно при выращивании спирулины используется питательная среда Заррук (Zarrouck, 1966), основным элементом которой является гидрокарбонат натрия (пищевая сода). Использование питательной среды Заррук для выращивания спирулины предполагает барботаж суспензии газо-воздушной смесью воздуха и СО2 (Zarrouck, 1966). Однако способность клеток спирулины выдерживать высокие величины рН позволяет культивировать спирулину без дополнительной подачи СО2, что значительно упрощает лабораторные исследования и удешевляет промышленное культивирование данного объекта.
Без дополнительной подачи СО2 в культуру единственным источником углерода является гидрокарбонт-ионы. Известно, что из-за высокого начального содержания соды в питательной среде именно поглощение гидрокарбонат-ионов клетками определяет динамику рН в накопительной культуре (Бородина, 2002). При высоких значениях рН среды (>11,5) углерод представлен в растворе только карбонат-ионами (Куприянова, Самылина, 2015), которые не поглощаются клетками спирулины, что приводит к остановке роста плотности культуры. Следует отметить, что рост культуры останавливается на плотностях около 1,5–2 г сухого веса (СВ)/л, в то время как среда Заррук по основным биогенным элементам (азот, фосфор и др.) рассчитана на 4,5 г СВ/л. Это означает, что в среде остается порядка половины всех питательны веществ, следовательно, при оптимальных световых условиях наступает лимитирование углеродом. Необходимым этапом оптимизации углеродного питания становится разработка математической модели роста водорослей как функции потока углерода.
В связи с этим целью данной работы являлось построение математической модели роста водоросли в накопительной культуре в условиях закрытой по углероду системы, а также адаптация параметров модели к культуре A. platensis.
Материалы и методы
Культура Arthrospira platensis (Nordstedt) Gomont была получена из коллекции Института морских биологических исследований им. А.О. Ковалевского (г. Севастополь). В качестве питательной среды использовали среду Заррук (Zarrouck, 1966). Лабораторная установка для культивирования состояла из фотобиореактора, системы освещения, термостабилизации. Эксперимент проводили в накопительном режиме культивирования. Фотобиореактор представлял собой ёмкость из стекла размером 500×250×10 (плоскопараллельный тип) с рабочей толщиной 1 см, рабочий объем реактора – 1 л. Сверху фотобиореактор закрывался пластиковой крышкой, в которой было выполнено отверстие для подачи воздуха. В качестве источника света использовалась лампа ДРЛ-750, расположенная на расстоянии 50 см от поверхности фотобиореактора и обеспечивающая среднюю освещённость 8 клк. Барботирование культуры осуществляли аквариумным компрессором, скорость подачи воздуха была установлена на уровне 0,55 л на литр культуры в минуту. Фотобиореактор был оснащен системой охлаждения («водяной рубашкой»), обеспечивающей поддержание температуры суспензии 27-28ºС.
В эксперименте проводили измерение температуры, рН, оптической плотности суспензии. Перед проведением измерений в фотобиореактор добавляли дистиллированную воду с целью компенсации испарения воды. Температуру суспензии измеряли ртутным термометром непосредственно в культиваторе, абсолютная погрешность измерений составляла ±0,5°С. Освещённость на поверхности фотобиореактора определяли люксметром Ю-116. Отбор проб для определения рН и оптической плотности проводили с помощью дозатора Biohit 1–5 мл с разных точек внутри фотобиореактора: отбирали по 5 мл суспензии и таким образом получали «среднюю пробу» объёмом 30 мл. Из средней пробы после её тщательного перемешивания отбирали 2 мл суспензии для определения оптической плотности. В остальном объёме измеряли рН с помощью иономера И-160М, абсолютная погрешность измерений составляла 0,01 единицы рН. Оптическую плотность рассчитывали по формуле: D = –lg(T), где Т – величина пропускания, определяемая при длине волны 750 нм, абсолютная погрешность при измерении величины пропускания не превышала 1%. Измерения проводили относительно дистиллированной воды. Следует отметить, что кюветы располагали максимально близко к фотоприёмнику, что позволяло снизить ошибку измерения оптической плотности культуры, связанную с увеличением светорассеяния при удалении от фотоприёмника (Геворгиз и др., 2005). При выходе показаний прибора за границы рабочего диапазона (от 30 до 70% пропускания), проба разбавлялась дистиллированной водой.
Математическая модель. Рассмотрим закрытую по углероду систему культивирования микроводорослей (Геворгиз и др., 2013). Примером такой системы может являться культивирование спирулины A. platensis на питательной среде Заррук без дополнительной продувки углекислым газом.
В простейшем случае накопительную кривую можно разделить на два участка, две фазы роста: фаза неограниченного роста и фаза лимитированного (ограниченного) роста. Согласно классическим представлениям (Blackman, 1905), на первом участке рост культуры происходит с максимальной удельной скоростью, величина которой зависит от организации узкого места метаболизма (Тренкеншу, 2005) и может определяться внешними световыми условиями (Лелеков, Тренкеншу, 2007). Математически скорость роста культуры A. platensisна данном участке записывается следующим образом:
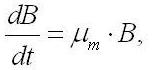
где µm – константа максимальной удельной скорости роста в данных условиях.
Проинтегрировав данное выражение при заданных начальных условиях, мы получим экспоненциальный рост плотности культуры во времени:

где В0 – начальная плотность культуры A. platensis в момент времени t=0.
Экспериментально доказано, что источниками неорганического углерода для низших фотоавтотрофов являются СО2 и НСО3– (Badger, Price, 2003; Price et al., 2008). Для культур, растущих при высоких значениях рН, углерод в среде может быть представлен только в виде гидрокарбонат- и карбонат-ионов. Существенную роль в ассимиляции углерода играет цинксодержащий фермент карбоангидраза, участвующий в различных стадиях работы СО2-концентрирующего механизма (Пронина, 2000). У цианобактерий внутриклеточная β-карбоангидраза ассоциирована с карбоксисомами (Самылина, 2008). В результате работы карбоангидразы на одну поглощенную молекулу НСО3– образуется одна молекула СО2 и один гидроксил-ион ОН– (Janson, Northen, 2010). СО2 используется в цикле Кальвина, а ОН– выносится во внешнюю среду, где взаимодействует с НСО3– с образованием СО32–. Таким образом изъятие углерода клетками в виде гидрокарбонат-иона приводит к образованию одной молекулы СО2, поступающей в цикл Кальвина, и карбонат-иона, который остается во внешней среде.
Так как содержание гидрокарбоната натрия в среде Заррук во много раз превышает содержание фосфата калия, то изменение рН культуральной среды будет определяться отношением концентраций карбонат- и гидрокарбонат-ионов. Пренебрегая всеми остальными процессами защелачивания (либо закисления за счёт органики) среды, запишем дифференциальное уравнение изменения молярной концентрации гидроксил-ионов:
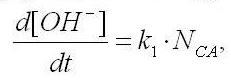
где k1 – константа связи, включающая активность и время оборота карбоангидразы; NCA – суммарное количество молекул карбоангидразы.
Считая долю карбоангидразы fCA в биомассе постоянной, можем выразить количество фермента через величину биомассы:
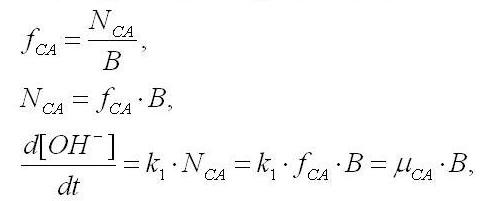
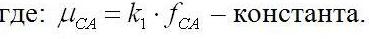
Учитывая то, что биомасса растет по экспоненциальному закону (1), последнее уравнение приобретет следующий вид:
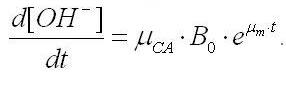
Начальному моменту времени t=0 соответствует некоторое начальное содержание гидроксил-ионов [ОН–]. Проинтегрируем последнее уравнение при данных начальных условиях:
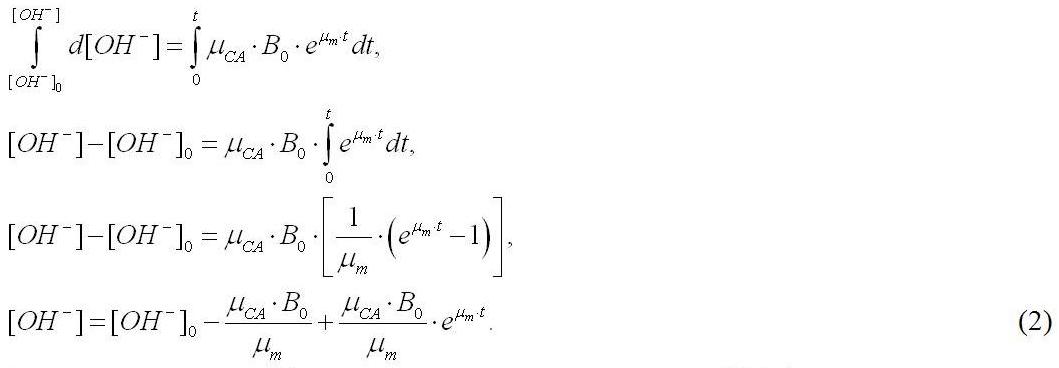
Анализ выражения (2) показывает, что концентрация [ОН–] в среде увеличивается экспоненциально. Это приводит к резкому увеличению рН среды на начальных этапах культивирования A. platensis, что подтверждается многочисленными экспериментальными данными. На рис.1 представлена накопительная кривая роста спирулины и динамика изменения рН культуральной среды.
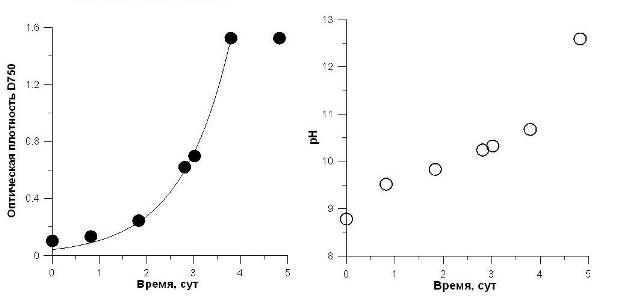
Рис. 1. Накопительная кривая роста и рН среды. Аппроксимация экспоненциальной фазы роста уравнением (1).
Плотность культуры увеличивалась в течение четырёх суток с последующим выходом в стационарную фазу. Благодаря отсутствию лимитирования светом, рост спирулины хорошо (R2 = 0,99) описывается экспоненциальным уравнением (1). Однако следует отметить небольшие отклонения от экспоненциального закона в самом начале накопительной кривой, что объясняется процессами фотоадаптации при переносе клеток с иннокулята с низкой на высокую освещенность (Геворгиз, Тренкеншу, 1998; Паламодова, 2009; Лелеков, Тренкеншу, 2010).
Параллельно с ростом культуры происходит увеличение рН среды. Математическую обработку данных по рН проводить довольно сложно, так как рН есть логарифм концентрации ионов водорода, концентрация которых, в свою очередь, будет меняться по экспоненте (2). Поэтому переведем величину рН среды в молярную концентрацию гидроксил-ионов:
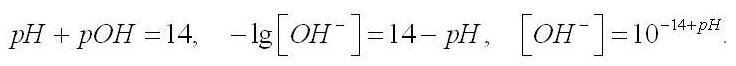
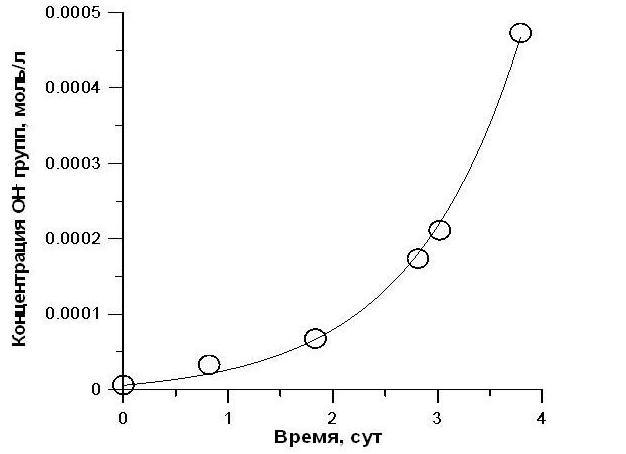
Рис. 2. Изменение концентрации гидроксил-ионов в среде. Аппроксимация экспериментальных данных уравнением (2).
Полученные результаты свидетельствуют об адекватности предложенной математической модели (R2 = 0,99). Следует отметить, что при проведении аппроксимации уравнением (2), мы использовали ранее определённое значение (см. рис. 1) максимальной удельной скорости роста, которое составило 0,95 сут-1. Значения начальных концентраций гидроксил-ионов и плотности культуры также являются экспериментально определяемыми величинами. Таким образом, единственным неизвестным параметром в уравнении (2) является коэффициент µCA, который, в свою очередь, является произведением содержания карбоангидразы в биомассе на её активность за время оборота. По нашим расчетам, в результате обработки экспериментальных данных (см. рис. 2) величина µCA составила 1,5× 10-4. Оценка данного параметра в дальнейших исследованиях может позволить сделать выводы о количестве и активности карбоангидразы в клетках различных видов низших фотоавтотрофов, выращиваемых в закрытой по углероду системе.
Представленная математическая модель позволяет получить уравнение, описывающее убыль гидрокарбонат-ионов в культуральной среде. Как показано выше, убыль их концентрации в среде будет определяется двумя процессами: отток на биосинтез, который происходит в ходе работы карбоангидразы, а также взаимодействие гидрокарбонат-ионов с гидроксильными группами, концентрация которых в растворе увеличивается экспоненциально согласно (2). Данные процессы можно формализовать в виде дифференциального уравнения:
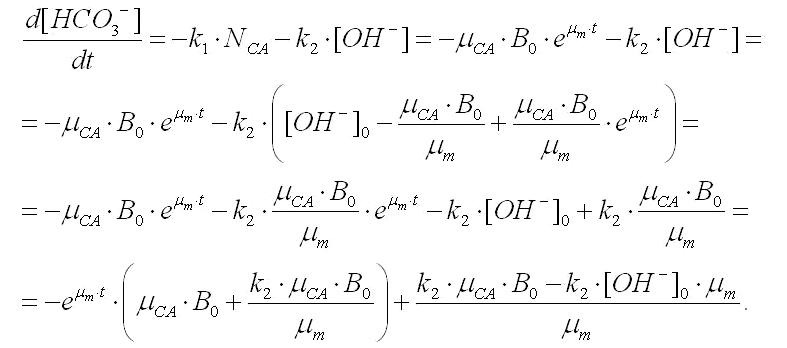
Последнее выражение интегрируется методом раздела переменных при начальных условиях t=0, 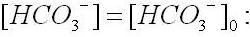
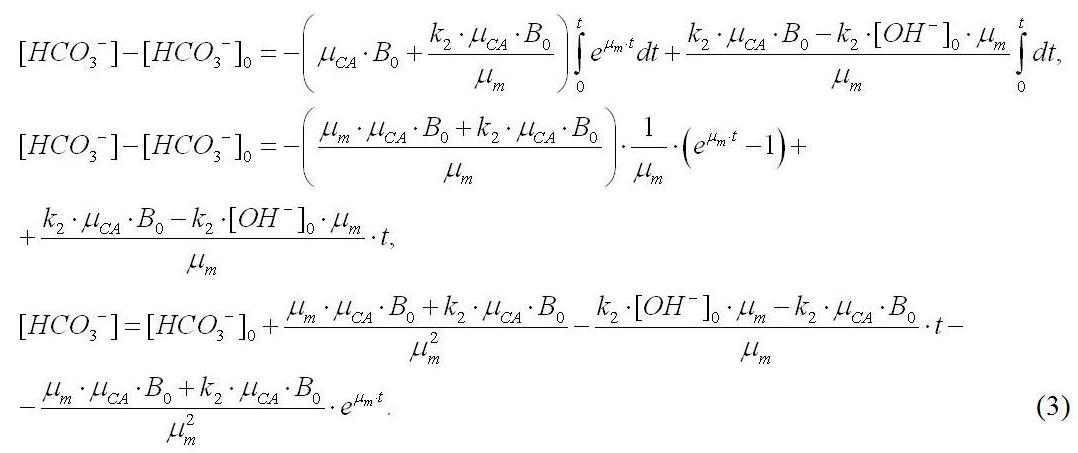
Выражение (3) позволяет описать динамику уменьшения концентрации гидрокарбонат-ионов в среде при заданных условиях. Все коэффициенты в (3), кроме константы пропорциональности k2, которая определяет активность перехода гидрокарбонат- в карбонат-ионы в присутствии [ОН–], есть либо измеряемые, либо расчётные величины, определяемые с помощью уравнений (1) и (2). Анализ (3) показывает, что концентрация гидрокарбонат-ионов снижается экспоненциально за счёт оттока на биосинтез, а также происходит её линейное уменьшение за счет взаимодействия со свободными гидроксил-ионами. Таким образом, часть доступного для биосинтеза углерода переходит в недоступную карбонатную форму. Этот факт позволяет ответить на поставленный в начале работы вопрос об остановке роста спирулины на плотностях, которые не менее чем в 2 раза ниже расчётных по прописи питательной среды Заррук.
Полученные уравнения (1) – (3) позволяют описать динамику роста плотности культуры, рН среды и концентрации НСО3– ионов только для условий неограниченного роста, т.е. для экспоненциальной фазы. С течением времени концентрация гидрокарбонатов, уменьшаясь по (3), достигнет некоторого значения, при котором дальнейший неограниченный рост по экспоненте невозможен. Культура перейдет в фазу замедления роста. Рост спирулины в случае лимитирования гидрокарбонат-ионами будет описываться следующей системой уравнений:
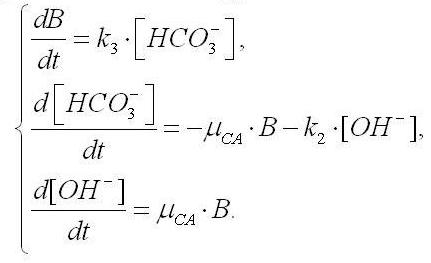
где k3 – константа, по смыслу являющаяся экономическим коэффициентом.
Для решения полученной системы уравнений и получения искомой зависимости биомассы спирулины от времени, продифференцируем первое уравнение два раза с последующей подстановкой в него второго и третьего уравнения системы:
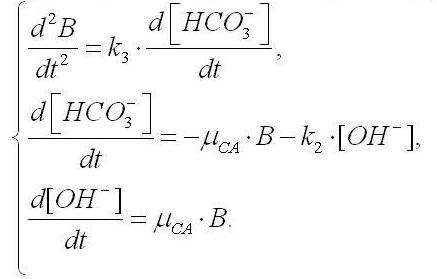
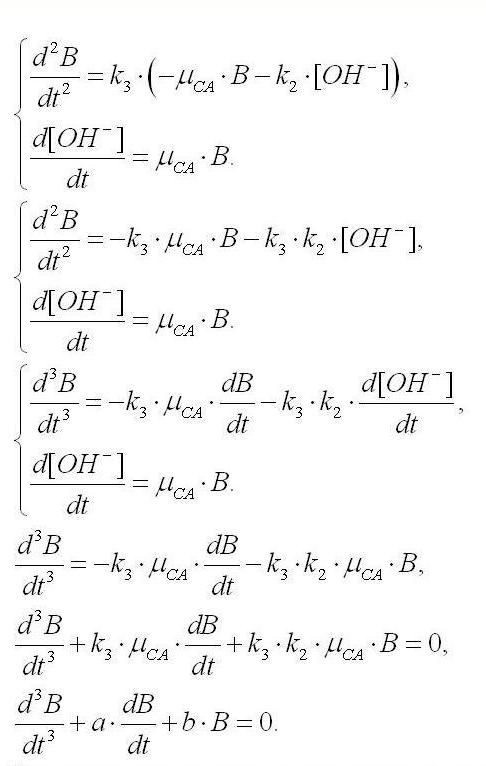
Решение последнего уравнения можно представить в виде:
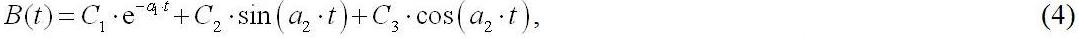
где а1, а2, а3 – обобщенные видоспецифичные кинетические коэффициенты, С1, С2, С3 – константы, которые можно найти из начальных и граничных условий.
Уравнение (4) применимо для описания динамики изменения плотности культуры спирулины в фазе замедления и стационарной фазе роста, когда наблюдается лимитирование углеродом. Отметим, что в (4) содержатся слагаемые, которые указывают на наличие периодических колебаний биомассы. Для спирулины в условиях закрытой по углероду системы такие колебания нами подтверждены экспериментально, причём как для биомассы, так и для рН среды (рис. 3). Сравнивая рисунок 3 A и 3 B, можно сделать заключение о синфазности колебаний плотности культуры и величины pH. Таким образом, периодическое изменение pH свидетельствует о наличии колебаний плотности культуры. Экспериментально показано (рис. 4), что колебания плотности являются затухающими и могут быть достаточно продолжительными.
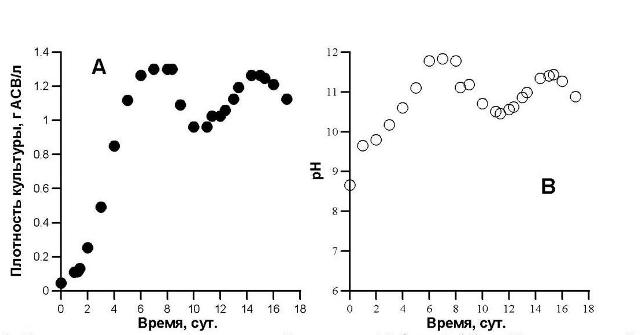
Рис. 3. Динамика плотности накопительной культуры A. platensis (А) и рН культуральной среды (В).
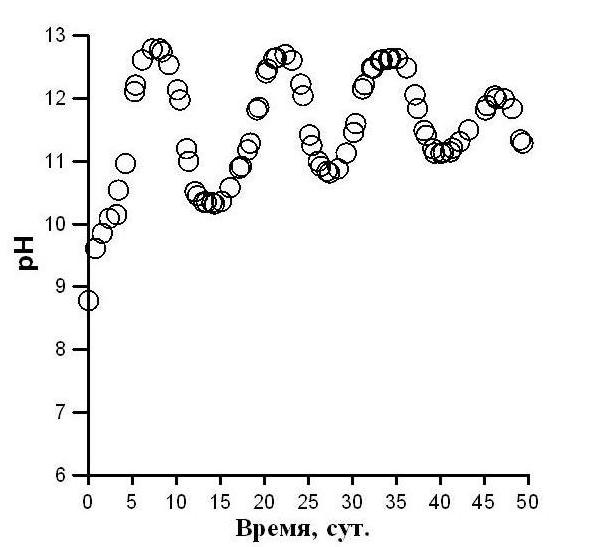
Рис. 4. Динамика рН среды накопительной культуры A. platensis.
Заключение
В работе предложена математическая модель, которая позволяет описать увеличение рН и уменьшение концентрации гидрокарбонат-ионов в культуральной среде с увеличением плотности культуры A. platensis, при условии, что углерод не вносится в фотобиореактор извне, т.е. система культивирования является закрытой по углероду. Модель достаточно точно описывает экспериментальные данные при экспоненциальном росте плотности культуры, а также позволяет объяснить колебания плотности культуры в стационарной фазе роста. акрытой по углероду системы такие колебания нами подтверждены экспериментально, причём как для биомассы, так и для рН среды (рис. 3). Сравнивая рисунок 3 A и 3 B, можно сделать заключение о синфазности колебаний плотности культуры и величины pH. Таким образом, периодическое изменение pH свидетельствует о наличии колебаний плотности культуры. Экспериментально показано (рис. 4), что колебания плотности являются затухающими и могут быть достаточно продолжительными.
Работа выполнена в рамках госзадания по НИР «Разработка научных основ решения гидробиологических и биотехнологических проблем интегрированного управления прибрежными зонами" № 1001-2014-0017
Список литературы
1. Бородина А.В. Динамика содержания карбонатов и гидрокарбонатов в среде Заррука при выращивании микроводоросли Spirulina platensis (Nords.) Geilt. в накопительной культуре // Экология моря. 2002. Вып.60. С. 48–52.
2. Геворгиз Р.Г., Алисиевич А.В., Шматок М.Г. Оценка биомассы Spirulina platensis (Nordst.) Geitl. по оптической плотности культуры // Экология моря. 2005. Вып.70. C. 96–106.
3. Геворгиз Р.Г., Лелеков А.С., Король О.Н. Моделирование динамики роста популяции микроорганизмов в накопительной культуре. Закрытая система // Рыбное хозяйство Украины. 2013. Т.5. С. 6–15.
4. Геворгиз Р.Г., Тренкеншу Р.П. Светозависимое содержание пигментов в микроводорослях. Стационарный процесс // Альгология. 1998. 8, №3. C. 273–277.
5. Куприянова Е.В., Самылина О.С. СО2-концентрирующий механизм и его особенности у галоалкалофильных цианобактерий // Микробиология. 2015. Т.84, №2. C. 144–159.
6. Лелеков А.С., Тренкеншу Р.П. Простейшие модели роста микроводорослей 4. Экспоненциальная и линейная фазы роста // Экология моря. 2007. Вып.74. C. 47–49.
7. Паламодова О.С. Динамика фотоадаптации некоторых видов диатомовых водорослей // Экология моря. 2009. Вып.78. С. 70–74.
8. Пронина Н.А. Организация и физиологическая роль СО2-концентрирующего механизма при фотосинтезе микроводорослей // Физиология растений. 2000. Т.47, №5. C. 801–810.
9. Самылина О.С. Углерод-концентрирующий механизм как компонент адаптации экстремально натронофильной цианобактерии Euhalothece natronophila к существованию в содовых озёрах: Автореф. дис. канд. биол. наук. – М., 2008. – 24 с.
10. Тренкеншу Р.П. Кинетика субстратзависимых реакций при различной организации метаболических систем. – Севастополь: ЭКОСИ-Гидрофизика, 2005. – 89 с.
11. Лелеков А.С., Тренкеншу Р.П. Моделирование динамики относительного содержания В-фикоэритрина и хлорофилла а в клетках Porphyridium purpureum и Spirulina platensis // Экология моря. 2010. Спец. вып. 81: Управление биосинтезом гидробионтов. C. 54–58.
12. Badger M. R., Price G.D. CO2-concentrating mechanisms in cyanobacteria: molecular components, their diversity and evolution // Journal of Experimental Botany. 2003. Vol.54, №383. P. 609–622.
13. Blackman F.F. Optima and limiting factors // Ann. Bot. Lond. 1905. 19. P. 281–295.
14. Janson Ch., Northen T. Calcifying cyanobacteria – the potential of biomineralization for carbon capture and storage // Current Opinion in Biotechnology. 2010. Vol.21. P. 365–371.
15. Price G.D., Badger M.R., Woodger F.J., Long B.M. Advances in understanding the cyanobacterial CO2-concentrating-mechanism (CCM): functional components, Ci transporters, diversity, genetic regulation and prospects or engineering into plants // Journal of Experimental Botany. 2008. Vol.59, №7. Р. 1441–1461.
16. Zarrouck C. Contribution a l’etude d’une cyanophycee. Influence de divers physiques et chimiques sur la crossance et la photosynthese de Spirulina maxima: Ph.D. thesis. – Paris, 1966. – 138 p.
Статья поступила в редакцию 9.12.2016
.
Modeling the dynamics of growth of Arthrospira (Spirulina) platensis and pH in a carbon closed system
A.S. Lelekov, R.G. Gevorgiz
A mathematical growth model of A. platensis batch culture in a closed carbon system is proposed. The model allows to explain the suspension of culture density while about half introduced carbon and other biogenic elements of the culture medium is availabled. It was shown that with the exponential culture growth the molar concentration of hydroxyl ions in the medium increased exponentially, while the concentration of bicarbonate ion decreased, not only exponentially, but linearly. The model is based on the well-known conceptions about cell carbon metabolism and carbon assimilation from the culture medium.
Key words: microalgae; mathematical model; pH of the culture medium; carbon limitation
Об авторах
Лелеков Александр Сергеевич - Lelekov Alexander S.
кандидат биологических наук
старший научный сотрудник, Институт морских биологических исследований имени А.О.Ковалевского РАН (ФГБУН ИМБИ), Севастополь, Россия (Federal State Institution of Science «The A.O.Kovalevsky Institute of Marine Biological Research of RAS» IMBR, Sevastopol, Russia), Отдел биотехнологий и фиторесурсов
a.lelekov@yandex.ru
Геворгиз Руслан Георгиевич - Gevorgiz Ruslan G.
кандидат биологических наук
старший научный сотрудник, Институт морских биологических исследований имени А.О.Ковалевского РАН (ФГБУН ИМБИ), Севастополь, Россия (Federal State Institution of Science «The A.O.Kovalevsky Institute of Marine Biological Research of RAS» IMBR, Sevastopol, Russia), Отдел биотехнологий и фиторесурсов
r-gevorgiz@yandex.ru
Корреспондентский адрес: Россия, 299011, Севастополь, пр. Нахимова, 2, ФГБУН ИМБИ, Отдел биотехнологий и фиторесурсов; тел. 88692550795.
ССЫЛКА НА СТАТЬЮ:
Лелеков А.С., Геворгиз Р. Г. Моделирование динамики роста Arthrospira (Spirulina) platensis и рН среды в закрытой по углероду системе // Вопросы современной альгологии. 2017. № 1 (13). URL: http://algology.ru/1113
Уважаемые коллеги! Если Вы хотите получить версию статьи в формате PDF, пожалуйста, напишите в редакцию, и мы ее вам с удовольствием пришлем бесплатно.
Адрес - info@algology.ru
При перепечатке ссылка на сайт обязательна
На ГЛАВНУЮ
Карта сайта
К разделу ОБЗОРЫ, СТАТЬИ И КРАТКИЕ СООБЩЕНИЯ

|